常用激活函数- Sigmoid - Tanh - ReLU - Softmax

发表于 更新于 Disqus：

sigmoid

表达式

$S(x)= \frac{1}{1+ e^{-x}}$

$S\prime (x)= \frac{e^{-x}}{(1+e^{-x})^2} = S(x)(1-S(x))$

曲线

sigmoid

1
2
3
4
5
6
7
8
9
10
11
12
13
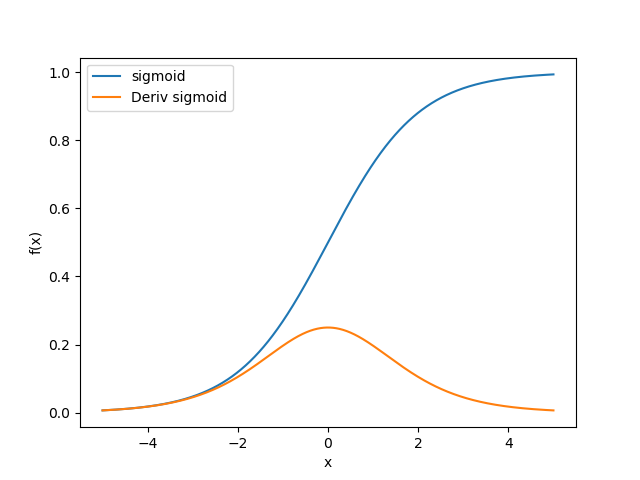
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-5,5,1000)  
y=[1/(1+np.exp(-i)) for i in x]
y=np.asarray(y)
y1=y*(1-y)
plt.plot(x,y,label='sigmoid')
plt.plot(x,y1, label='Deriv sigmoid')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='best')
plt.show()

优缺点

优点

  1. 求导容易
  2. 输出范围有限(0,1), 所以数据在传递的过程中不容易发散.

缺点

  1. 函数饱和使得梯度消失, 从而无法有效更新参数.
  2. 函数输出为非零对称的(输出恒大于0), 从而导致梯度在反向传播中全部为正或者全部为负, 使得更新呈现”Z”字型.
  3. 复杂的幂运算耗时严重.

tanh

表达式

$tanh(x)= \frac{sinh(x)}{cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

$tanh\prime (x) = 1- tanh^2(x)$

曲线

tanh

1
2
3
4
5
6
7
8
9
10
11
12
13
14
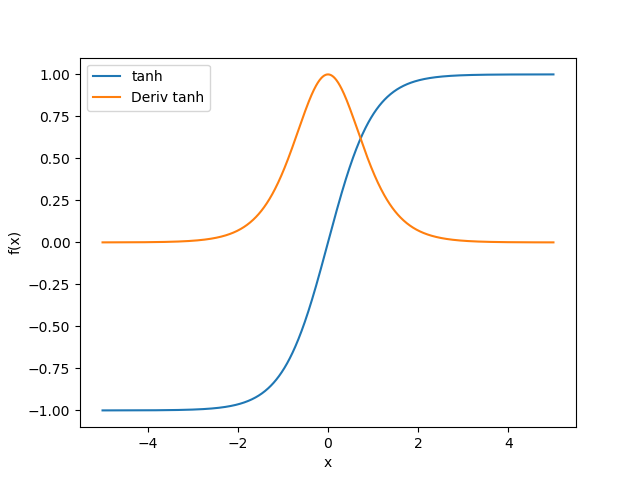
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-5,5,1000)  
temp1=pow(np.e,x)
temp2=pow(np.e,-x)
y=(temp1-temp2)/(temp1+temp2)
y1=1-y*y

plt.plot(x,y,label='tanh')
plt.plot(x,y1, label='Deriv tanh')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='best')
plt.show()

优缺点

优点

  1. 收敛速度快(相对于sigmoid)
  2. 不存在非零对称问题

缺点

  1. 函数饱和使得梯度消失, 从而无法有效更新参数.
  2. 复杂的幂运算耗时严重.

ReLU

ReLU(Rectified Linear Unit), 整流线性单位函数, 也称修正线性单元. 通常指以斜坡函数及其变种为代表的非线性函数.

表达式

$$f(x) = max(0,x)$$

$$
f(x)=
\begin{cases}
1 & if \quad x>0 \\
0 & otherwise
\end{cases}
$$

曲线

ReLU

1
2
3
4
5
6
7
8
9
10
11
12
13
14
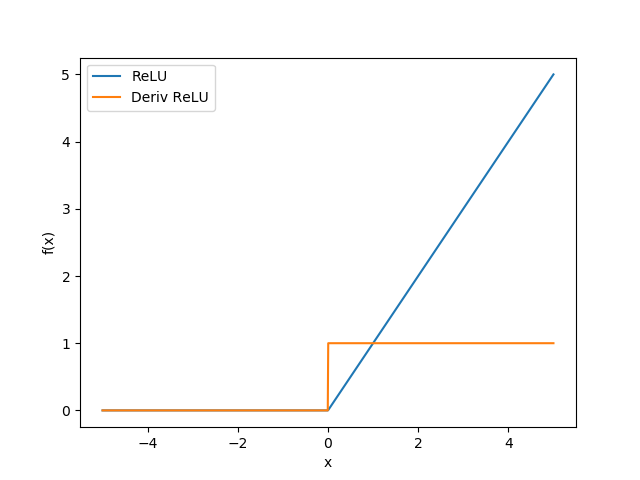
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-5,5,1000)
y=np.zeros_like(x)
y=np.where(x>0, x, y )
y1=np.where(x>0, 1, 0 )

plt.plot(x,y,label='ReLU')
plt.plot(x,y1, label='Deriv ReLU')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='best')
plt.show()

优缺点

优点

  1. 没有饱和区, 不存在梯度消失问题.
  2. 没有复杂的指数运算, 计算简单、效率提高.
  3. 实际收敛速度较快, 大约是 Sigmoid/tanh 的 6 倍.
  4. 比 Sigmoid 更符合生物学神经激活机制.

缺点

  1. 函数输出为非零对称
  2. Dead ReLU Problem(神经元坏死问题): 某些神经元可能永远不会被激活, 导致相应参数永远不会被更新(当x小于0时, 梯度为0). 产生这种现象的两个原因: 参数初始化问题; learning  rate太高导致在训练过程中参数更新太大. 解决方法: 采用Xavier初始化方法, 以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法.
  3. ReLU不会对数据做幅度压缩, 所以数据的幅度会随着模型层数的增加不断扩张.

ReLU的变种版

之所以叫变种而不是升级, 是因为在某些情况下可以超越ReLU, 但是在有些情况下则无效.

Leaky ReLU

表达式

$f(x) = max(0.01x,x)$

为了解决Dead ReLU Problem, 将ReLU的前半段设为$0.01x$.

ELU(Exponential Linear Units)

表达式

$$
f(x)=
\begin{cases}
x & if \quad x>0 \\
\alpha(e^x -1) & otherwise
\end{cases}
$$

softmax

softmax 函数, 可以称之为归一化指数函数, 其一般应用于多分类问题(输出层激励函数)

它能将一个含人鱼实数的$K$维向量$Z$”压缩”到另一维实向量$\sigma(Z)$中, 使得每个元素的范围都在$(0,1)$之间, 并且所有元素和为1.

$\sigma (z)_j = \frac{e^{z_j}}{\sum _{k=1}^K e^{z_k}} \quad for j=1,2, \cdots, K$

基本概念

函数饱和

假设$f(x)$为在实数域上的函数

  1. 当$x$趋近于正无穷, 函数$f(x)$趋近于0, 那么将其称之为右饱和. $\lim \limits_{x \rightarrow +\infty} {f\prime(x) } = 0$

  2. 当$x$趋近于负无穷, 函数$f(x)$趋近于0, 那么将其称之为左饱和. $\lim \limits_{x \rightarrow -\infty} {f\prime(x) } = 0$

  3. 当一个函数既满足左饱和又满足右饱和的时候我们就称之为饱和, 典型的函数有Sigmoid, Tanh函数.

  4. 对于任意的$x$, 如果存在常数$c$, 当$x>c$时, $f(x) \equiv 0$, 则称其为右硬饱和. 相反的, 如果存在常数$c$, 当$x<c$时, $f(x) \equiv 0$, 则称其为左硬饱和. 既满足左硬饱和又满足右硬饱和的我们称这种函数为硬饱和.

  5. 对于任意的$x$, 如果存在常数$c$, 当$x>c$时, 恒有$f\prime (x)$趋近于0, 则称其为右软饱和, 相反的, 如果存在常数$c$, 当$x<c$时, 恒有$f\prime (x)$趋近于0,则称其为左软饱和. 既满足左软饱和又满足右软饱和的我们称这种函数为软饱和.

线性关系(函数) & 非线性关系(函数)

在现代学术界中, 线性关系一词存在2种不同的含义.

  1. 若某数学函数或数量关系的函数图形呈现为一条直线或线段, 那么这种关系就是一种线性的关系.
    定义: $f(x)$是个只拥有一个变数的一阶多项式函数, 即是可以表示为 $ f(x)=kx+b $的形式(其中$k,b$为常数).

  2. 在代数学和数学分析学中, 如果一种运算同时满足特定的”加性”和”齐性”, 则称这种运算是线性的.
    定义: $f(x)$具有两个性质: 可加性 $f(x+t) = f(x) + f(t)$, 一次齐次性 $f(mx) = mf(x)$

非线性关系(函数)是指除了线性关系(函数)以为的其他函数, 指数函数, 对数函数, 幂函数, 多项式函数等.