Apriori算法
算法介绍
Apriori算法是R.Agrawal和R.Srikant于1994年提出的为布尔关联规则挖掘频繁项集的原创性算法。算法基于这样的事实:算法使用频繁项集性质的先验知识。Apriori使用一种称作逐层搜索的迭代方法,$k$项集用于探索$(k+1)$项集。首先,通过扫描数据库,累积每个项的计数,并收集满足最小支持度的项,找出频繁$1$项集的集合,该集合记做$L_1$。然后,$L_1$用于找频繁$2$项集的集合$L_2$,$L_2$用于找$L_3$,如此下去,直到不能再找到频繁$k$项集。
Apriori性质:频繁项集的所有非空子集也必须是频繁的。
利用Apriori算法找出频繁项集需要两个步骤,连接和剪枝
连接
为找$L_k$,通过将$L_{k-1}$与自身连接产生候选$k$项集的集合。该候选项集合记作$C_k$。设$l_1$和$l_2$是$L_{k-1}$中的项集。记号$l_i[j]$表示$l_i$中的第$j$项(例如,$l_1[k-2]$表示$l_1$的倒数第二项)。为方便起见,Apriori假定事务或项集中的项按照字典次序排序。对于$(k-1)$项集$l_1$,意味将项排序,使$l_i[1]<l_i[2]<\cdots<l_i[k-1]$。执行连接$L_{k-1}\bowtie L_{k-1}$,如果它们的前$(k-2)$个项相同的话,那么$L_{k-1}$的元素是可连接的(即,如果$$(l_1[1]=l_2[1])\wedge(l_1[2]=l_2[2])\wedge\cdots\wedge(l_1[k-2]=l_2[k-2])\wedge(l_1[k-1]<l_2[k-1])$$,那么$L_{k-1}$的元素$l_1$和$l_2$是可连接的)。条件$(l_1[k-1]<l_2[k-1])$仅仅是保证不产生重复。连接$l_1$和$l_2$产生的结果项集是$l_1[1],l_1[2],\cdots,l_1[k-1],l_2[k-1]$。
剪枝
$C_k$是$L_k$的超集,也就是说,$C_k$的成员可以是频繁也可以不是频繁的,但所有的频繁$k$项集都包含在$C_k$中。扫描数据库,确定$C_k$中每个候选的计数,从而确定$L_k$(即根据定义,计数值不小于最小支持度计数的所有候选是频繁的,从而属于$L_k$)。然而,$C_k$可能很大,这样所涉及的计算量就很大。为了压缩$C_k$,可使用Apriori性质。任何非频繁的$(k-1)$项集都不是频繁$k$项集的子集。因此,如果候选$k$项集的$(k-1)$项子集不在$L_{k-1}$中,则该候选也不可能是频繁的,从而可以从$C_k$中删除。这种子集测试可以使用所有频繁项集的散列树快速完成。
实例演示
下表为AllElectronics某分店的实物数据
| TID | 商品ID的列表 |
|---|---|
| T100 | I1,I2,I5 |
| T200 | I2,I4 |
| T300 | I2,I3 |
| T400 | I1,I2,I4 |
| T500 | I1,I3 |
| T600 | I2,I3 |
| T700 | I1,I3 |
| T800 | I1,I2,I3,I5 |
| T900 | I1,I2,I3 |
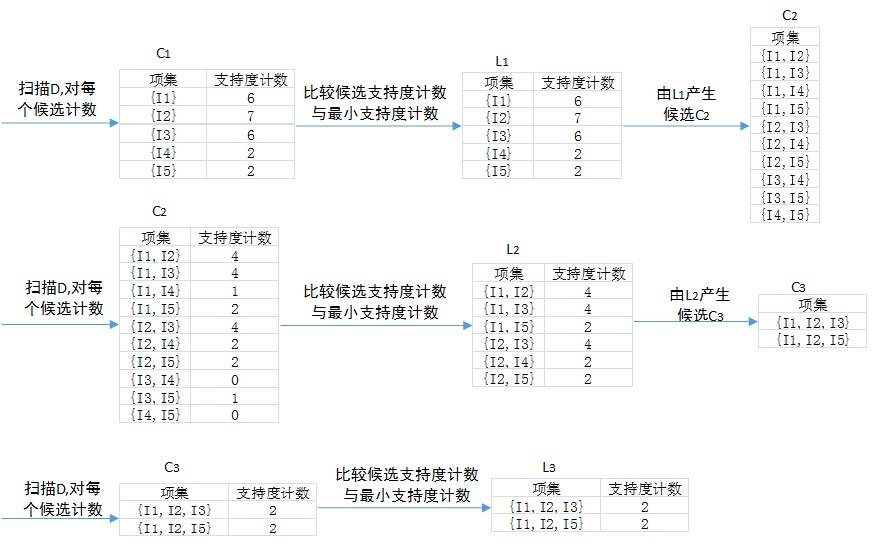
- 在算法的每一次迭代,每项都是候选1项集的集合$C_1$的成员。算法简单地扫描所有的事务,对每项的出现次数计数。
- 假定要求最小支持度计数为2,即$min\_sup=2$(这里谈论的是绝对支持度,使用的是支持度计数,对应的相对支持度为$2/9=22\%$)。可以确定频繁$1$项集的集合$L_1$。它由满足最小支持度的候选$1$项集组成。在我们的例子中,$C_1$中所有候选都满足最小支持度。
- 为发现频繁$2$项集的集合$L_2$,算法使用$L_1\bowtie L_1$产生候选$2$项集的集合$C_2$。$C_2$由$C_{|L_1|}^{2}$个$2$项集组成。
注意:在剪枝步,没有候选从$C_2$中删除,因为这些候选的每个子集都是频繁的。
4. 继续扫描$D$中的事务,计算$C_2$中每个候选项集的支持度计数。
5. 确定频繁$2$项集的集合$L_2$,它由满足最小支持度的$C_2$中的候选$2$项集组成。
6. 候选$3$项集的集合$C_3$的产生详细在下图中。从连接步,首先令
$C_3=L_2\bowtie L_2 \{ \{I1,I2,I3 \} , \{ I1,I2,I5 \} , \{ I1,I3,I5 \} , \{ I2,I3,I4 \} , \{ I2,I3,I5 \} , \{ I2,I4,I5 \} \}$
根据Apriori性质,频繁项集的所有子集也必须是频繁的,可以确定后4个候选不可能是频繁的。因此,把它们从$C_3$中删除,这样,在此后扫描$D$确定$L_3$时就不必再求它们的计数值。
注意:由于Apriori算法使用逐层搜索技术,给定候选$k$项集,只需要检查它们的$k-1$个子集是否频繁。
a. 连接:
$C_3=L_2\bowtie L_2 = \{ \{ I1,I2 \} , \{ I1,I3 \} , \{ I1,I5 \} , \{ I2,I3 \} , \{ I2,I4 \} , \{ I2,I5 \} \} \bowtie$
$ \{ \{ I1,I2 \} , \{ I1,I3 \} , \{ I1,I5 \} , \{ I2,I3 \} , \{ I2,I4 \} , \{ I2,I5 \} \} $
$= \{ \{ I1,I2,I3 \} , \{ I1,I2,I5 \} , \{ I1,I3,I5 \} , \{ I2,I3,I4 \} , \{ I2,I3,I5 \} \{ I2,I4,I5 \} \} $
b.剪枝:使用Apriori性质剪枝,频繁项集的所有非空子集也必须是非频繁的。
- $\{ I1,I2,I3 \}$的$2$项子集是$\{ I1,I2\} , \{ I1,I3\}$ 和 $ \{ I1,I2\}$。$\{ I1,I2,I3 \}$的所有$2$项子集都是$L_2$的元素。因此,$\{ I1,I2,I3 \}$保留在$C_3$中。
- $\{ I1,I2,I5 \}$的$2$项子集是$\{ I1,I2\} , \{ I1,I5\}$ 和 $ \{ I2,I5\}$。$\{ I1,I2,I5 \}$的所有$2$项子集都是$L_2$的元素。因此,$\{ I1,I2,I5 \}$保留在$C_3$中。
- $\{ I1,I3,I5 \}$的$2$项子集是$\{ I1,I3\} , \{ I1,I5\}$ 和 $ \{ I3,I5\}$。$\{ I3,I5 \}$不是$L_2$的元素。因而不是频繁的。因此,从$C_3$中删除,$\{ I1,I3,I5 \}$保留在中。
其他的也都是一样,通过这样的步骤去判断。
最终$C_3=\{ \{ I1,I2,I3 \} , \{ I1,I2,I5 \} \}$
- 扫描$D$中的事务确定$L_3$,它由满足最小支持度的$C_3$中的候选$3$项集组成。
- 算法使用$L_3\bowtie L_3$产生候选$4$项集的集合$C_4$。尽管连接产生结果$\{ \{ I1,I2,I3,I5 \} \}$,但是这个项集被剪去,因为它的子集$\{ I2,I3,I5 \}$不是频繁的。这样,$C_4=\emptyset$,算法终止,找出了所有的频繁项集。